NYU K12 STEM Education: Machine Learning (Day 7)

nyu-header

Images in Computer

  • Images are stored as arrays of quantized numbers in computers

Gray Scale Images

  • Gray scale image: 2D matrices with each entry specifying the intensity (brightness) of a pixel
  • Pixel values range from 0 to 255, 0 being the darkest, 255 being the brightest
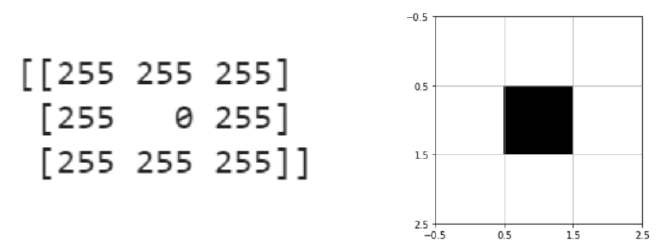
Figure 1: Grayscale Image
Figure 1: Grayscale Image

Color Images:

  • Color image: 3D array, 2 dimensions for space, 1 dimension for color
  • Can be thought of as three 2D matrices stacked together into a cube, each 2D matrix specify the amount of each color: Red,Green, Blue value at each pixel
Figure 2: Color Image
Figure 2: Color Image

Limits of Fully Connected Network

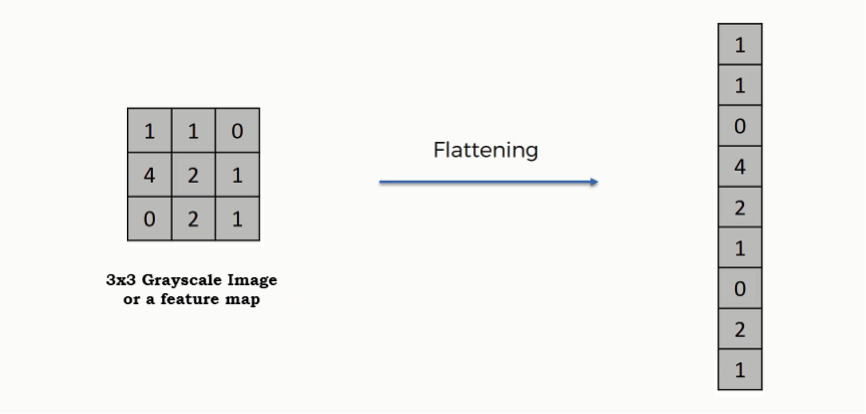
  • In MNIST, we used a fully connected network, in which each neuron in the hidden layer is connected to all \(28 \times 28 = 784\) pixels
  • Higher definition images often contain millions of pixels \(\rightarrow \) It is not practical to use fully connected network
  • Fully connected network treat each individual pixel as a feature, it does not utilize the positional relationship between pixels
Figure 3: Flattening an Image
Figure 3: Flattening an Image

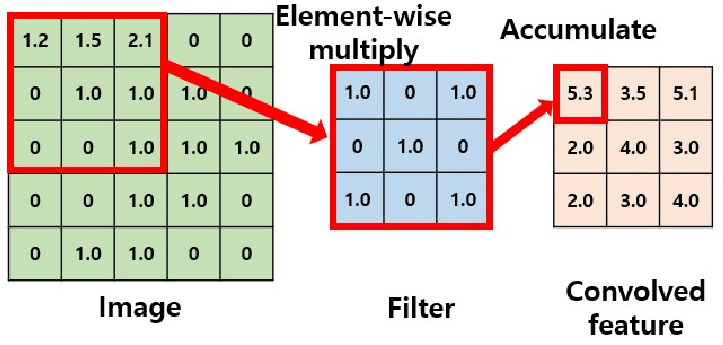
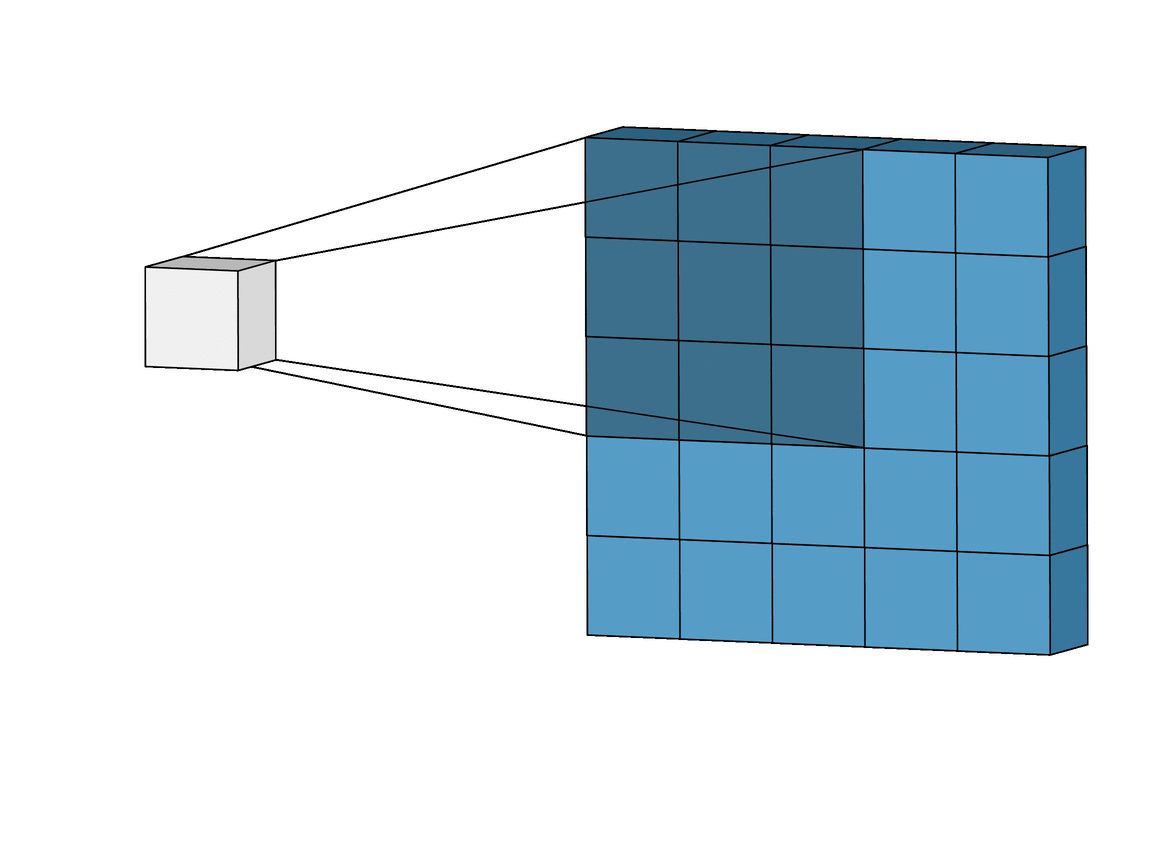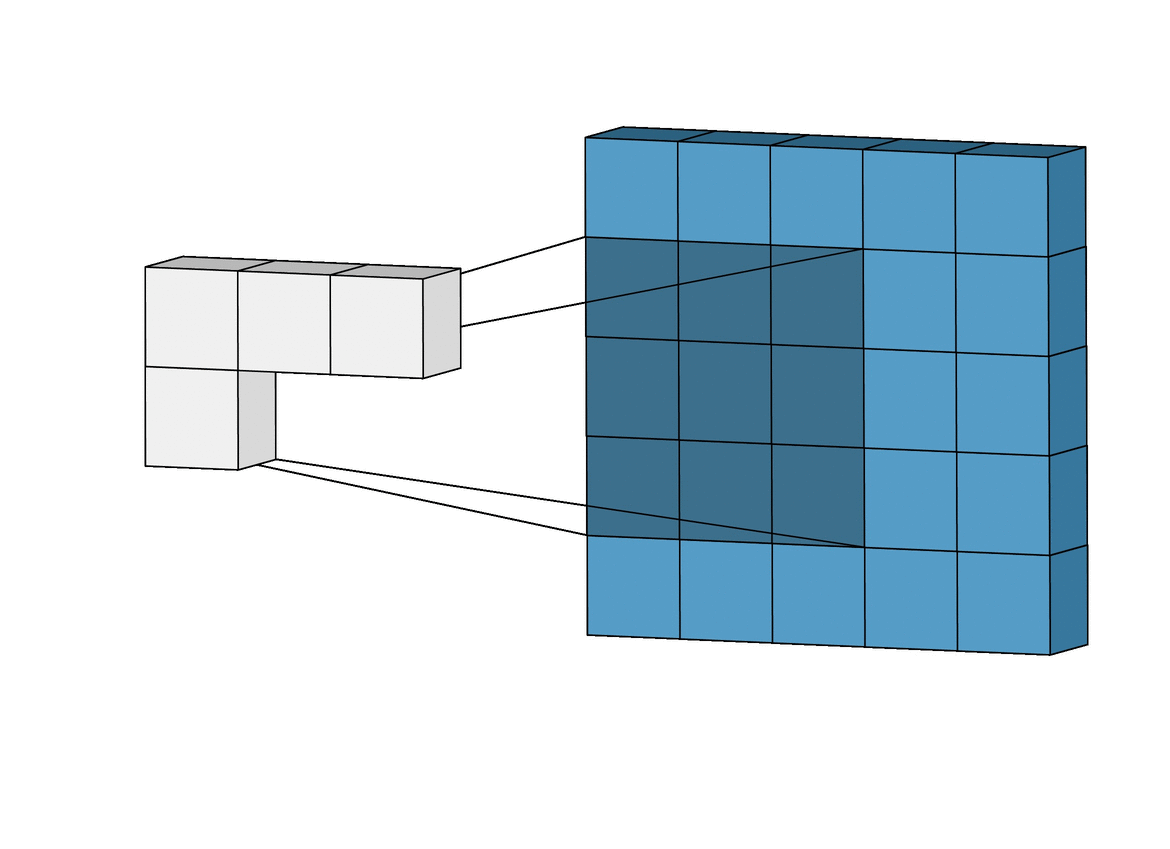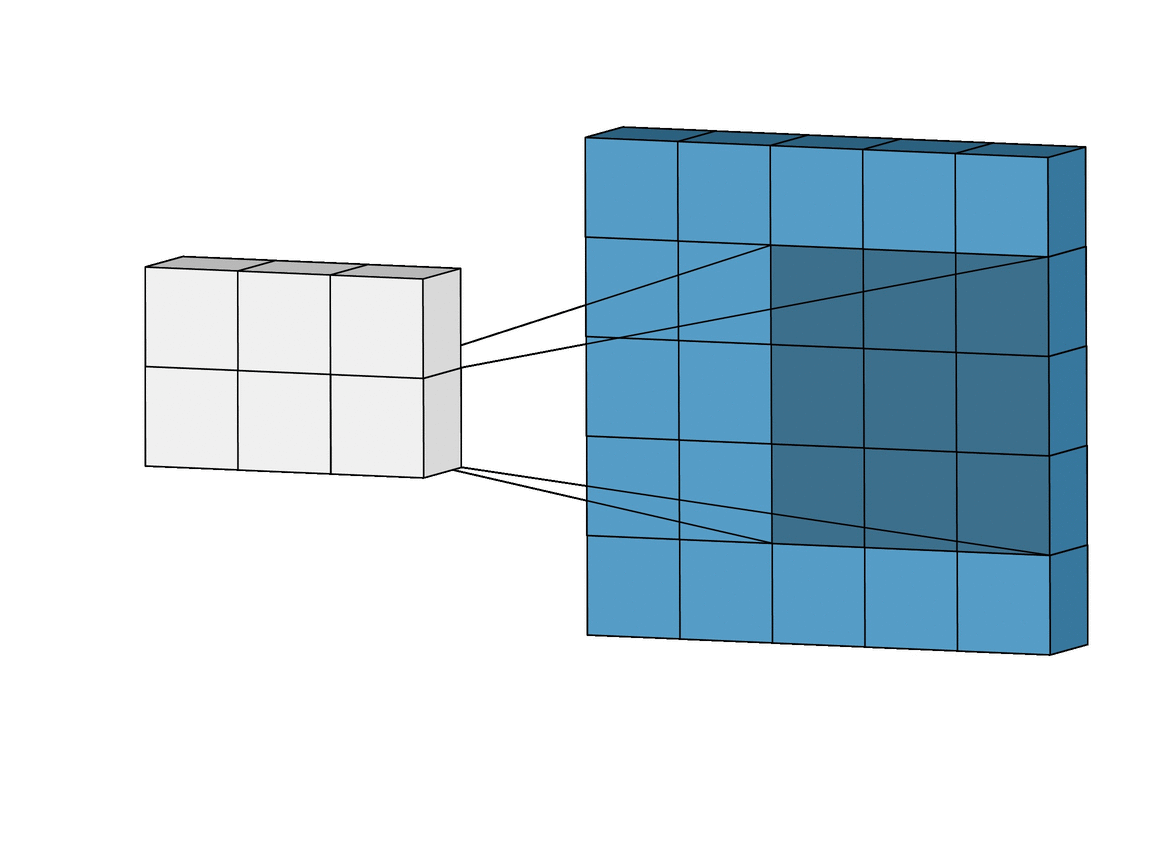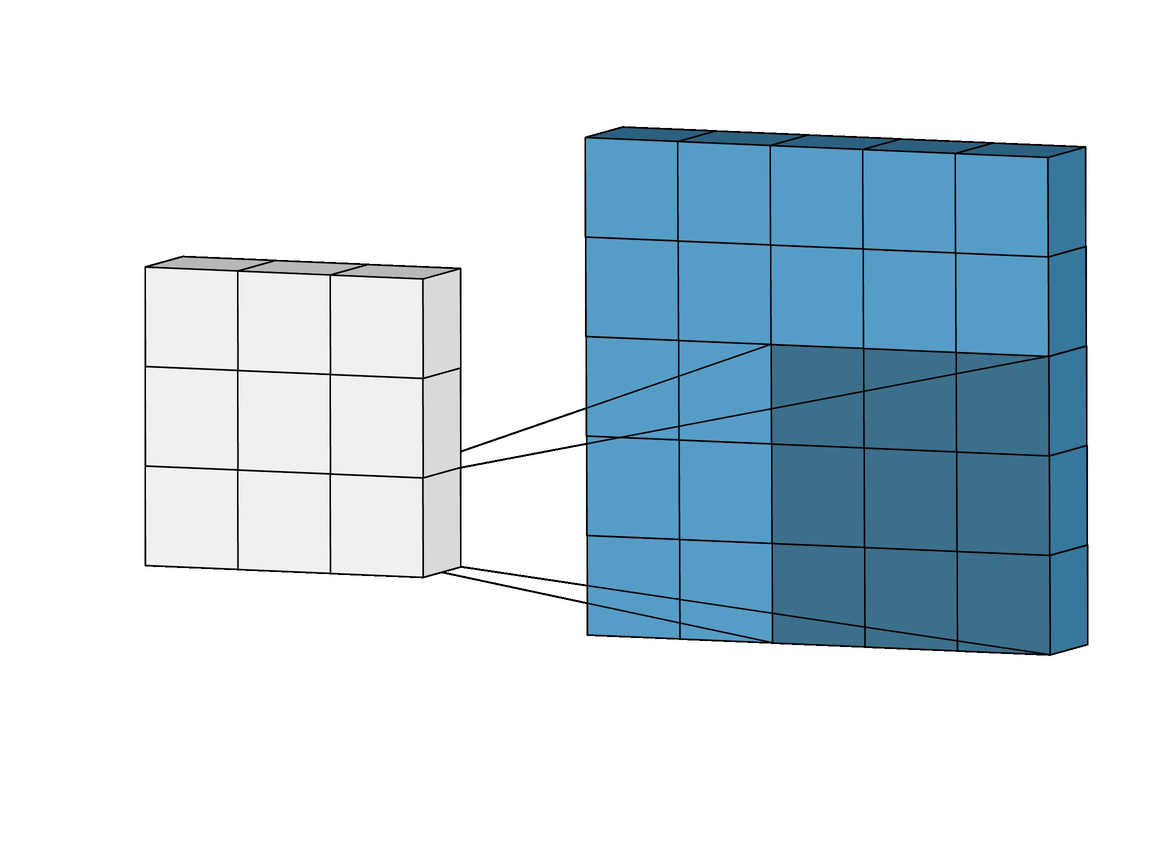
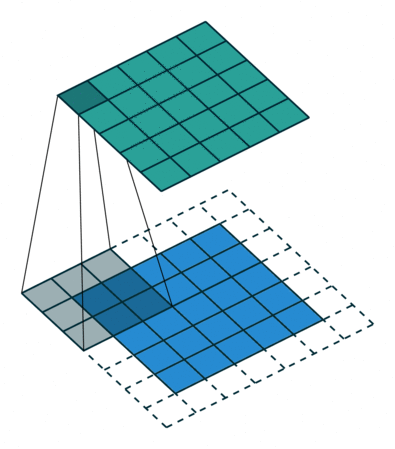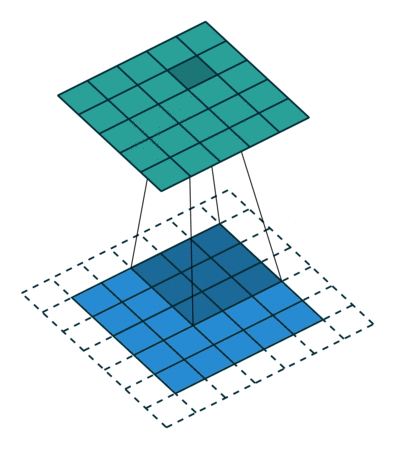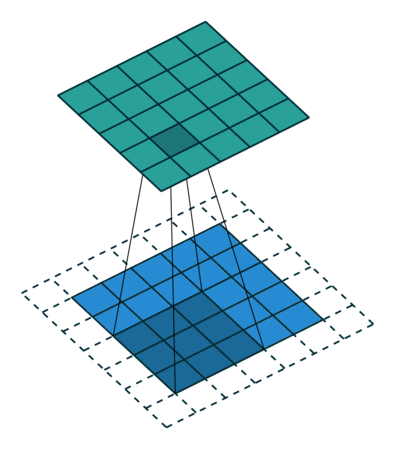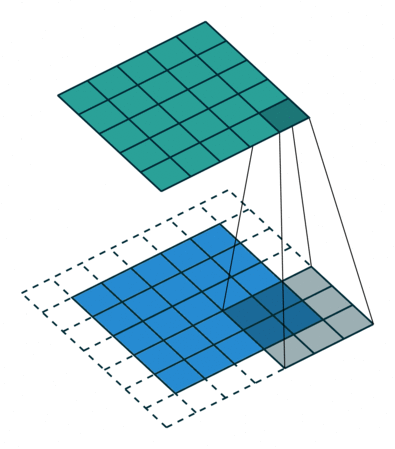
Convolution

An operation on an image(matrix) X with a kernel W

\[ Z = X \circledast W \]

Figure 4: Convolution Operation
Figure 4: Convolution Operation

Why Convolution?

  • With convolution, each output pixel depends on only the neighboring pixels in the input
  • This allows us to learn the positional relationship between pixels
  • Use of different kernels allows us to detect features
Figure 5: Convolution Visualization
Figure 5: Convolution Visualization
Figure 6: Convolution with Padding - Visualization
Figure 6: Convolution with Padding - Visualization

Convolution for Multiple Channels

  • A kernel for each channel. Could be same kernel, or different
  • Perform a convolution for each of the channel, with the respective kernel
  • Sum the results
Figure 7: Convolution across channels
Figure 7: Convolution across channels

Max-pooling

  • Down-samples the inputs
  • Provides translation invariance. Why?
  • Apply after activation!
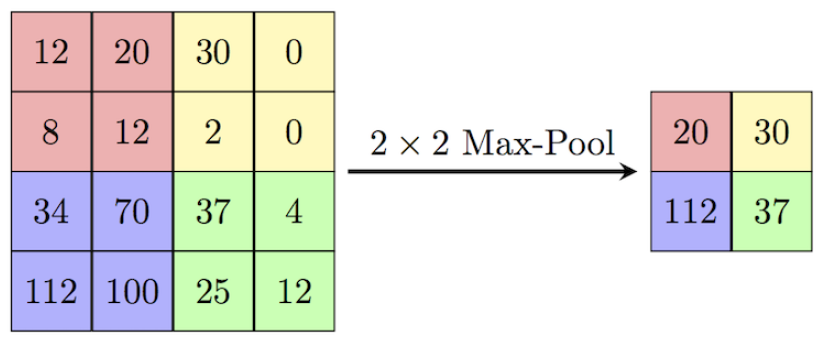
Figure 8: Max-pooling
Figure 8: Max-pooling

Data-augmentation

  • Image classification is a difficult task
  • We need more data!
  • Labeling is expensive and time-consuming.
  • How can we create new images?

Examples:

  • Mirroring
Figure 9: Mirroring
Figure 9: Mirroring
  • Rotation and Translation
Figure 10: Rotation and Translation
Figure 10: Rotation and Translation
  • Random Cropping
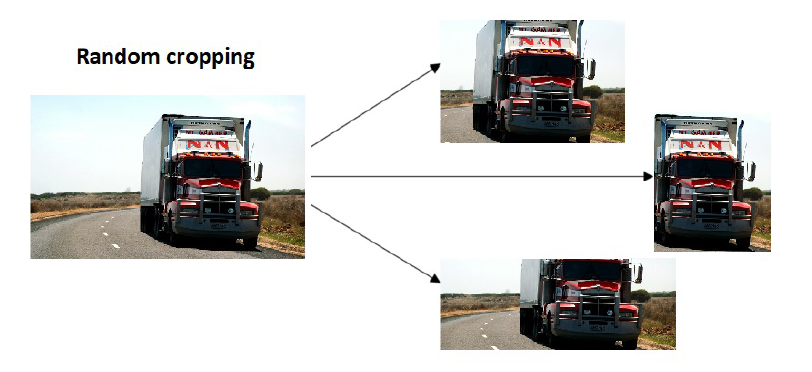
Figure 11: Random Cropping
Figure 11: Random Cropping
  • Color Shifting
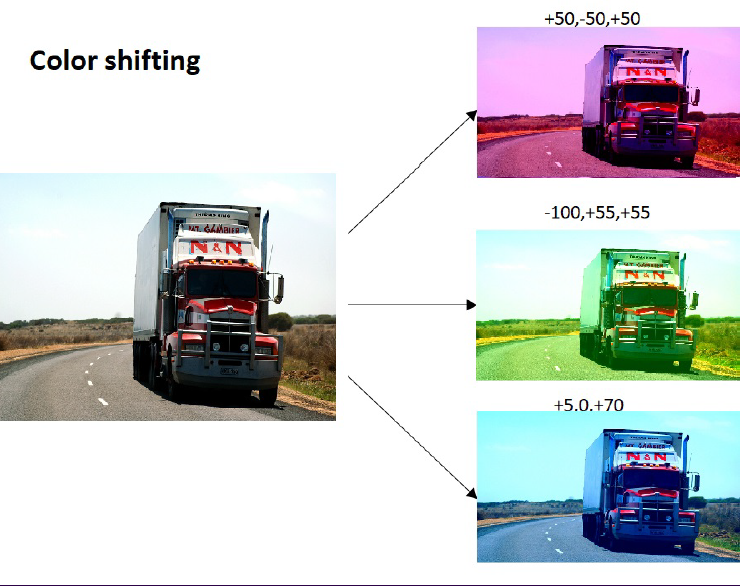
Figure 12: Color Shifting
Figure 12: Color Shifting

Data Normalization

  • Given the dataset \((x_i, y_i) \) for \(i = 1, 2, \cdots, N\)

  • Mean:

    \[ \bar{x} = \frac{1}{N} \sum^{N}_{i=1} x_i \]

  • Variance:

    \[ \sigma^{2} = \frac{1}{N} \sum^{N}_{i=1} (x_i - \bar{x})^{2} \]

  • Standard deviation:

    \[ \sigma = \sqrt{\sigma^2} \]

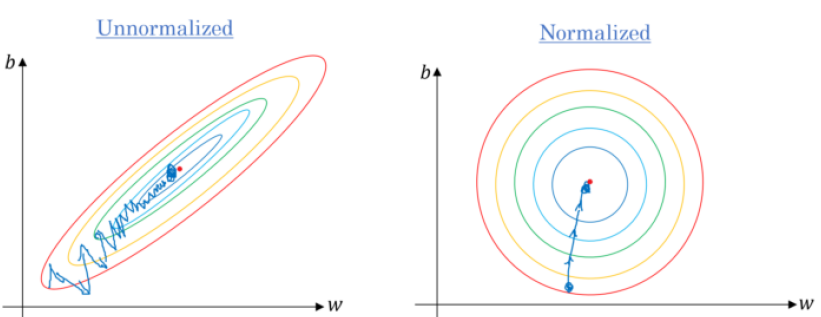
  • Normalization : Replace each \(x_i\) by \(x_i’ = \frac{x_i - \bar{x}}{\sigma} \)
  • The new dataset will have a mean of \(0\) and a variance of \(1\).
Figure 13: Unnormalized Gradient Descent vs. Normalized Gradient Descent
Figure 13: Unnormalized Gradient Descent vs. Normalized Gradient Descent

Batch Normalization

  • We normalize the inputs to the network. Why not do that for the inputs to the hidden layers?
  • Batch norm: normalize the inputs to a layer for each mini-batch.
  • Apply before activation!

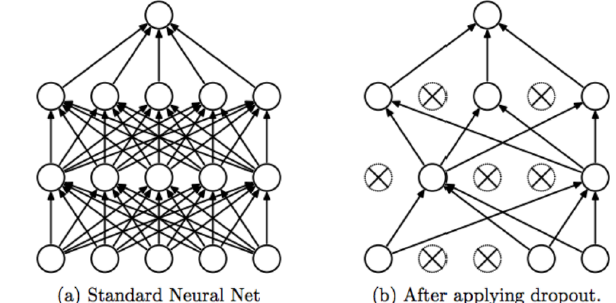
Dropout

  • Patented by Google
  • Randomly disable neurons and their connections between each other.
  • Reduce complex co-adaptive relationships between neurons.
  • This is the same as using a neural network with the same amount of layers but less neurons per layer.
  • The more neurons the more powerful the neural network is, and the more likely it is to overfit.
  • This also means that the model can not rely on any single feature, therefore would need to spread out the weights.
Figure 14: Dropout
Figure 14: Dropout

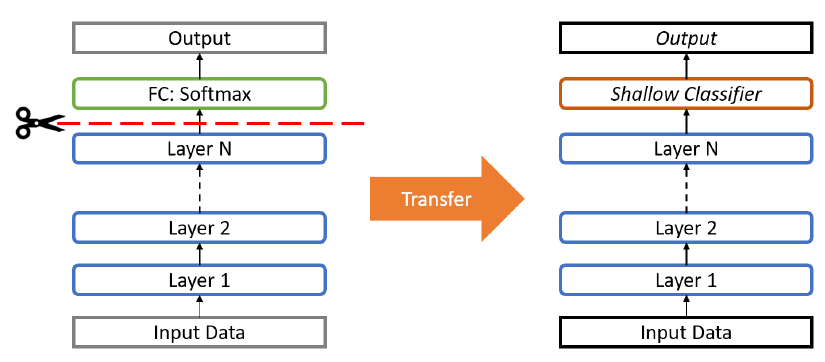
Transfer Learning

  • You can freeze the early layers and replace the last few layers to match your own application needs (e.g. different number of classes, different activation functions).
  • Only train the replaced layers and use the weights of the early layers ”as-is”.
  • This is similar to transferring the knowledge from one network to another, thus the name transfer learning.
Figure 15: Transfer Learning
Figure 15: Transfer Learning

Demos

  1. Images in Computer
  2. Kernels Example
  3. CNN Example
  4. MNIST Classifier
  5. Cats and Dog

References