NYU K12 STEM Education: Machine Learning (Day 6)

nyu-header

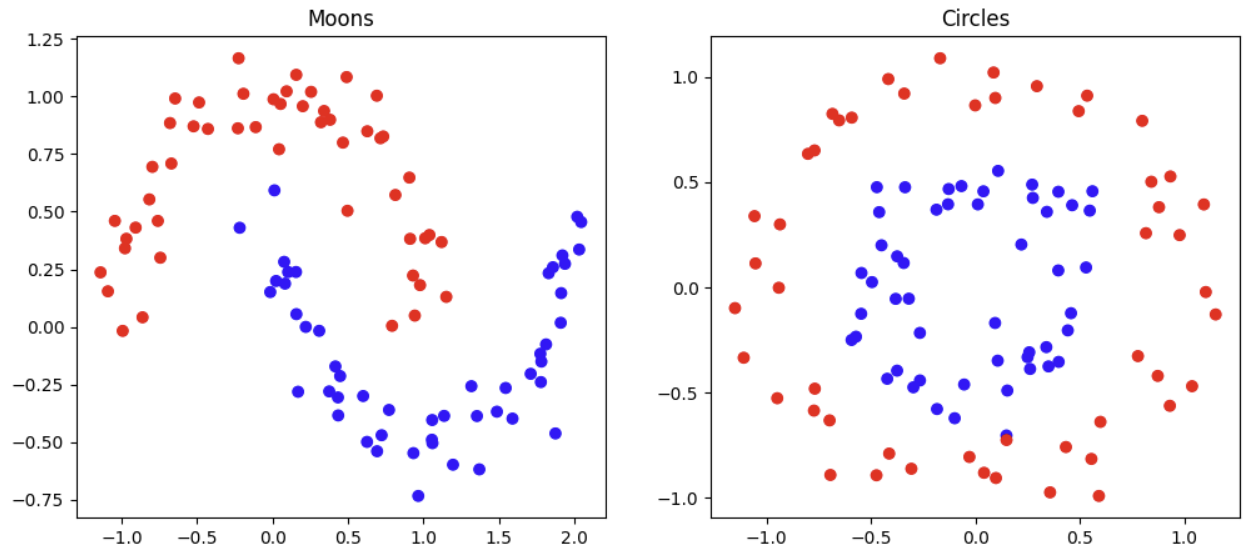
Limitations of Linear Classifiers

  • Much more complex dataset are difficult to classify with simple classifiers
Figure 1: Complex Datasets
Figure 1: Complex Datasets

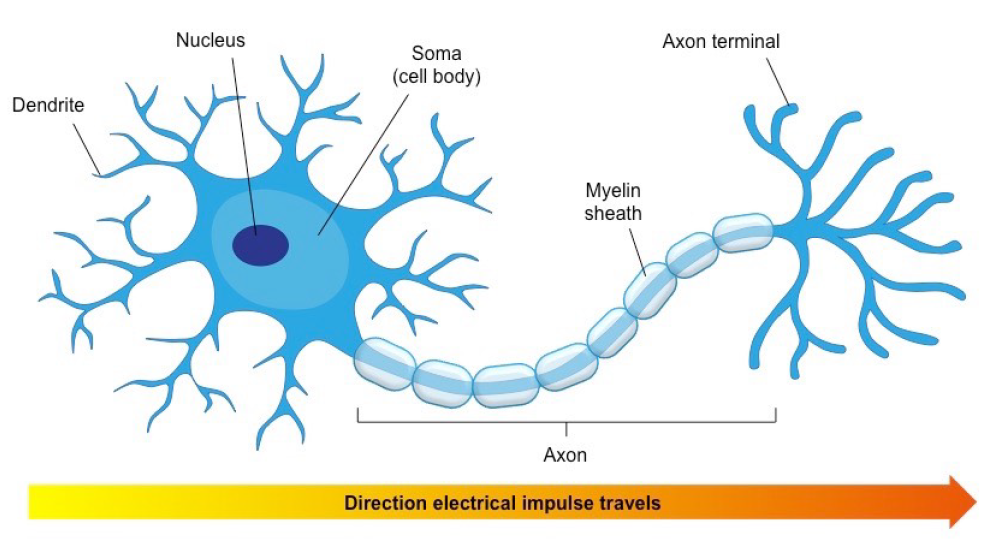
Neuron

Biological Neuron

  • A neuron can receive electrochemical signals from other neurons;
  • A neuron fires once its accumulated electric charge passes a certain threshold.
  • Neurons that fire together wire together.
Figure 2: Biological Neuron
Figure 2: Biological Neuron

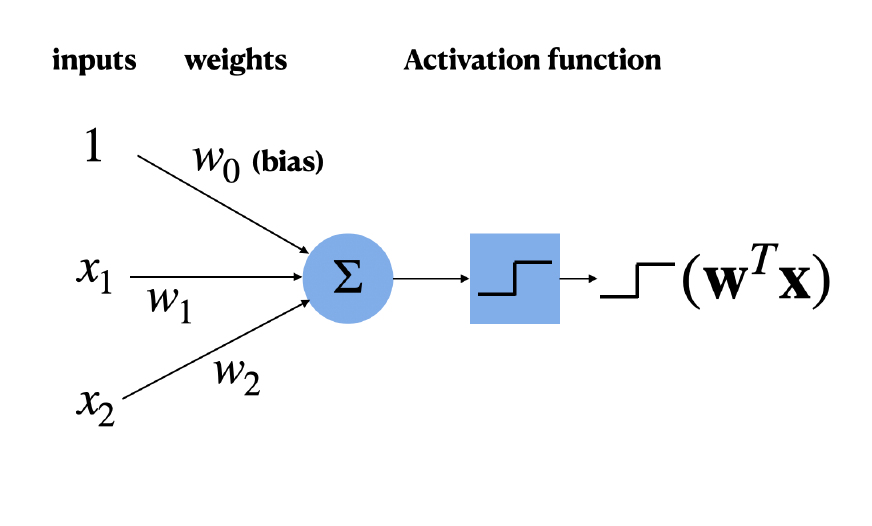
Mathematical Neuron - Perceptron

Figure 3: Mathematical Neuron
Figure 3: Mathematical Neuron

Relation to Logistic Regression

  • What if we use the sigmoid function as the activation?

    \[ f(x) = \sigma(w^Tx) \]

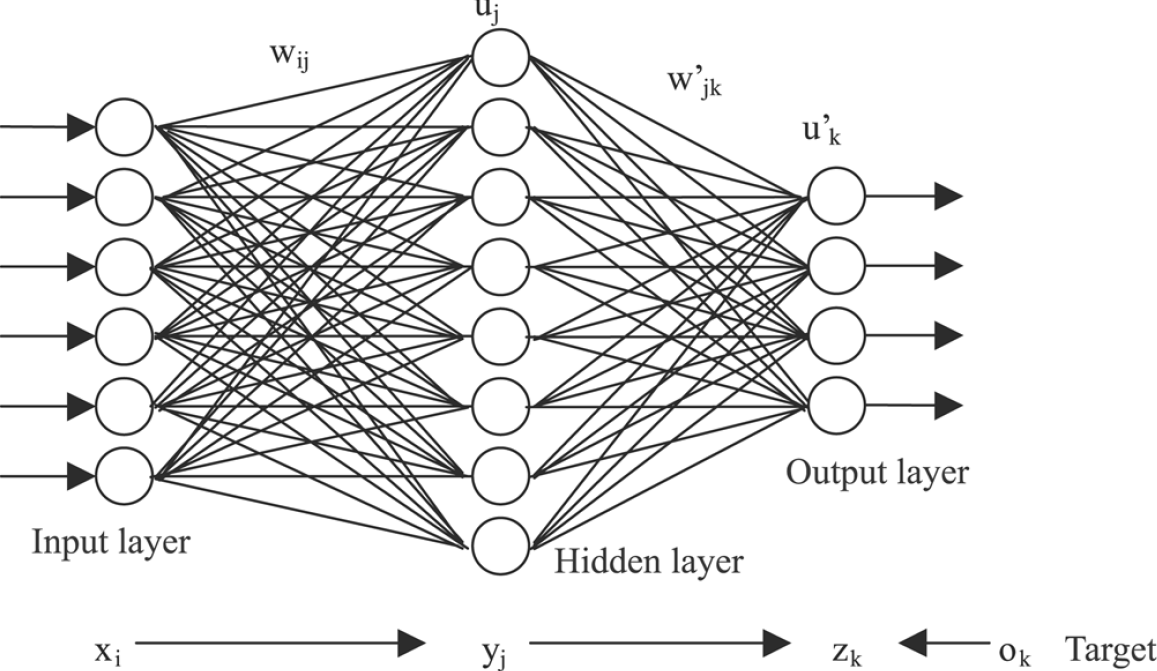
Multi-layer Perceptron (MLP)

  • We need more neurons and we need to connect them together!
    • Many ways to do that…
    • Today: multi-layer perceptron/fully connected feed-forward network.

MLP Example

Figure 3: Multilayer Perceptron
Figure 3: Multilayer Perceptron

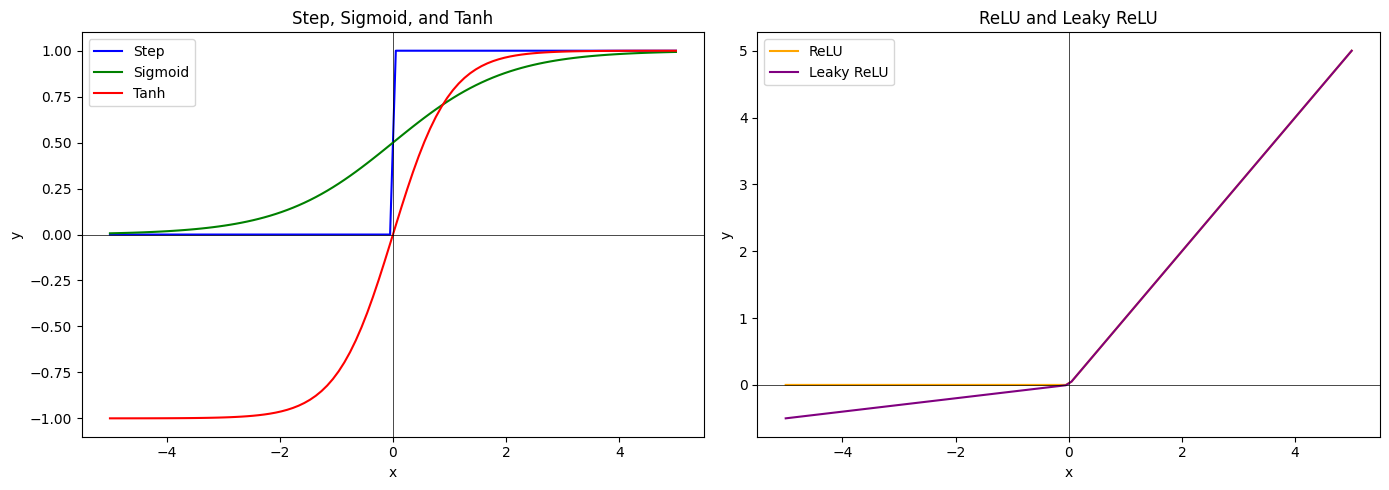
Activation Functions

  • Different activation functions have different impact on the behaviour of the neuron.
Figure 4: Activation Functions
Figure 4: Activation Functions

Deep Neural Network

Figure 5: Simple vs. Deep Neural Networks
Figure 5: Simple vs. Deep Neural Networks

More about MLPs

  • Many choices for the activation function: Sigmoid, Tanh, ReLU, Softmax, etc.
  • Many choices for the number of hidden layers and the number of neurons per layer.
  • MLPs can approximate any continuous function given enough data.
  • MLPs can overfit, but we know many effective ways of regularization.

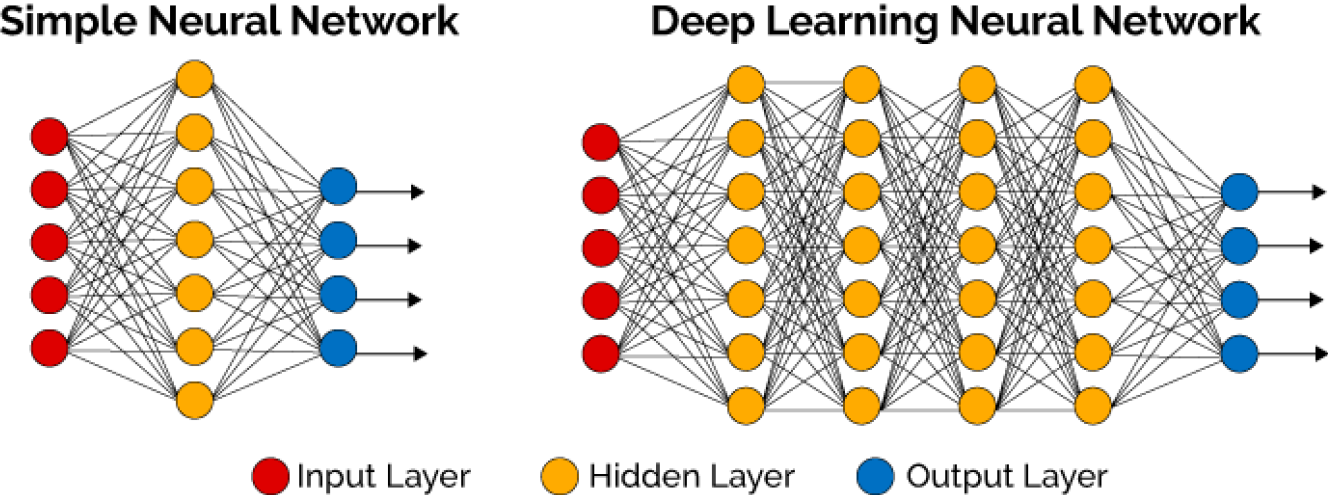
Deep Learning

  • What does deep learning mean?
    • Deep: Neural network architectures with many hidden layers.
    • Learning: Optimizing model parameters given a dataset.
  • In general, the deeper the model is, the more parameters we need to learn and the more data is needed.

Large-scale Machine Learning

  • For deep learning systems to perform well, large datasets are required
    • COCO 330K images
    • ImageNet 14 million images
  • Challenges:
    • Memory limitation: GeForce RTX 2080 Ti has 11 GB memory, while ImageNet is about 300 GB.
    • Computation: Calculating gradients for the whole dataset is computationally expensive (slow), and we need to do this many times.

Stochastic Gradient Descent

  • Idea: Instead of calculating the gradients from the whole dataset, do it only on a subset.
    • Randomly select \(B\) samples from the dataset
    • The loss for this subset

    \[ \hat{J}(w) = \frac{1}{B} \sum^{B}_{i=1} ||y_i - \hat{y_i}||^2 \]

    • Update Rule:

    \[ \text{Repeat\{} \\ \: w_{\text{new}} = w - \alpha \nabla \hat{J}(w) \\ \text{\}} \]

  • This gives a noisy gradient:

    \[ \nabla \hat{J}(w) = \nabla J(w) + \epsilon \]

  • SGD: \(B = 1\), gives very noisy gradients
  • (batch) GD: \(B = N, \epsilon = 0\), expensive to compute
  • Mini-batch GD: Pick a small \(B\), typical values are 32, 64, rarely more than 128 for image inputs
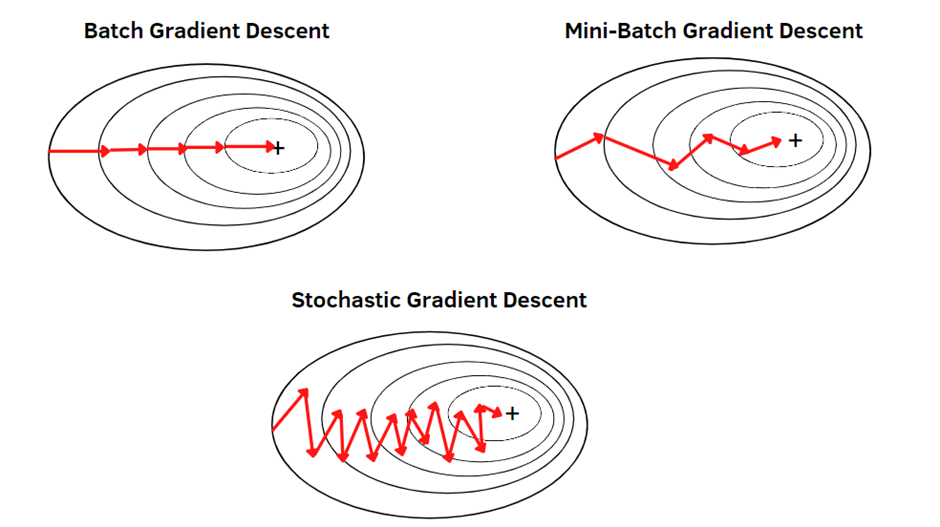
Figure 5: GD, MBGD, SGD
Figure 5: GD, MBGD, SGD

Some Noise Helps

  • Even if we can, we rarely set \(B = N\). In fact, some noise in the gradients might help to
    • escape from local minima,
    • escape from saddle points, and
    • improve generalization

Overparameterized Models

  • Modern deep learning models are heavily overparameterized, i.e. the number of learnable parameters is much larger than the number of the training samples.
    • ResNet: State-of-the-art vision model, 10-60 million parameters
    • GPT-3: State-of-the-art language model, 175 billion parameters
  • Conventional wisdom: Such models overfit.
  • It is not the case in practice!

Demos

  1. Keras Basics
  2. Fish Market with MLP

References