NYU K12 STEM Education: Machine Learning (Day 4)

nyu-header

Classification

Given the dataset \((x_i , y_i)\) for \(i = 1, 2, \cdots , N\) , find a function \(f (x )\) (model) so that it can predict the label \(\hat{y}\) for some input \(x\), even if it is not in the dataset, i.e. \(\hat{y} = f (x)\)

  • Positive : \(y = 1\)
  • Negative : \(y = 0\)
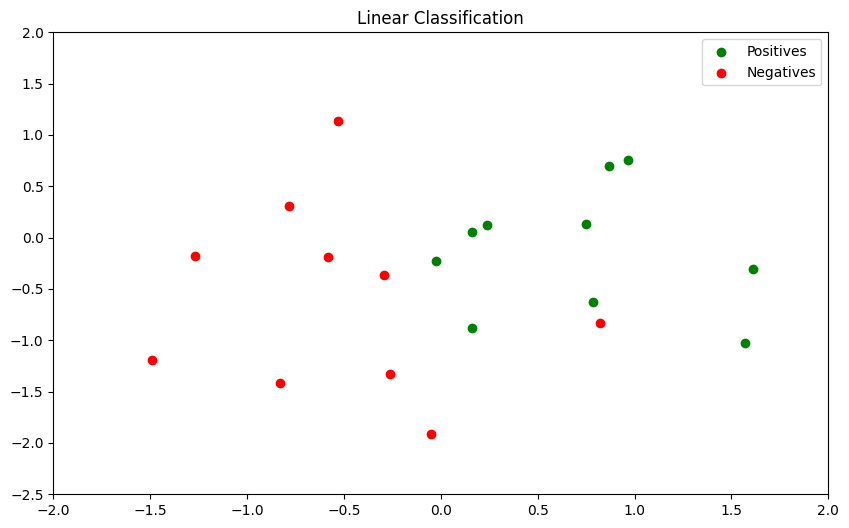
Figure 1: Linear Classification
Figure 1: Linear Classification

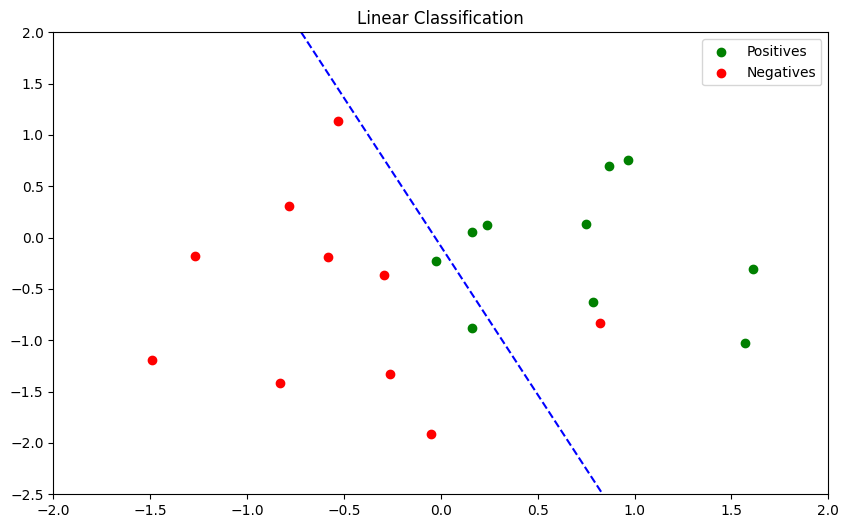
Decision Boundary

  • Evaluation metric :

    \[ \text{Accuracy} = \frac{\text{Number of correct prediction}}{\text{Total number of prediction}} \]

Figure 2: Decision Boundary Visualization
Figure 2: Decision Boundary Visualization

Need for a new model

  • What would happen if we used the linear regression model:

    \[ \hat{y} = w_0 + w_1x \]

  • \(y\) is \(0\) or \(1\)
  • \(\hat{y}\) will take any value between \(-\infty\) and \(\infty\)
  • It will be hard to find \(w_0\) and \(w_1\) that make the prediction \(\hat{y}\) match the label \(y\)

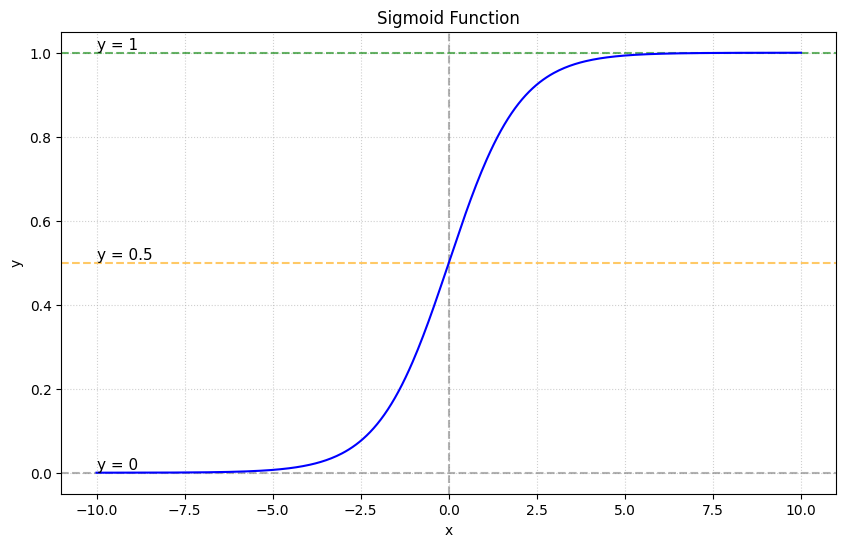
Sigmoid Function

  • By appling the sigmoid function, we enforce \(0 \le \hat{y} \le 1\)

    \[ \hat{y} = \text{sigmoid}(w_0 + w_1x) = \frac{1}{1 + e^{-(w_0 + w_1x)}} \]

Figure 3: Sigmoid Function
Figure 3: Sigmoid Function

Binary Cross Entropy Loss

  • Binary Cross Entropy Loss:

    \[ \text{Loss} = \frac{1}{N} \sum^{N}_{i=1} \left[ -y_i \log \hat{y_i} - (1 - y_i) \log (1 - \hat{y_i}) \right] \]

  • If \(y_i = 0\):

    \[ \left[ -y_i \log \hat{y_i} - (1 - y_i) \log (1 - \hat{y_i}) \right] = - \log (1 - \hat{y_i}) \]

  • If \(y_i = 1\):

    \[ \left[ -y_i \log \hat{y_i} - (1 - y_i) \log (1 - \hat{y_i}) \right] = - \log (\hat{y_i}) \]

MSE vs Binary Cross Entropy Loss

  • MSE of a logistic function has many local minima
  • The Binary Cross Entropy loss has only one minimum

Classifier

\[ \hat{y} = \text{sigmoid}(w_0 + w_1x) = \frac{1}{1 + e^{-(w_0 + w_1x)}} \]

  • How to deal with uncertainty?
    • Thanks to the sigmoid, \(\hat{y} = f (x)\) is between \(0\) and \(1\)
    • If \(\hat{y}\) is close to \(0\), the data is probably negative
    • If \(\hat{y}\) is close to \(1\), the data is probably positive
    • If \(\hat{y}\) is around \(0.5\), we are not sure.
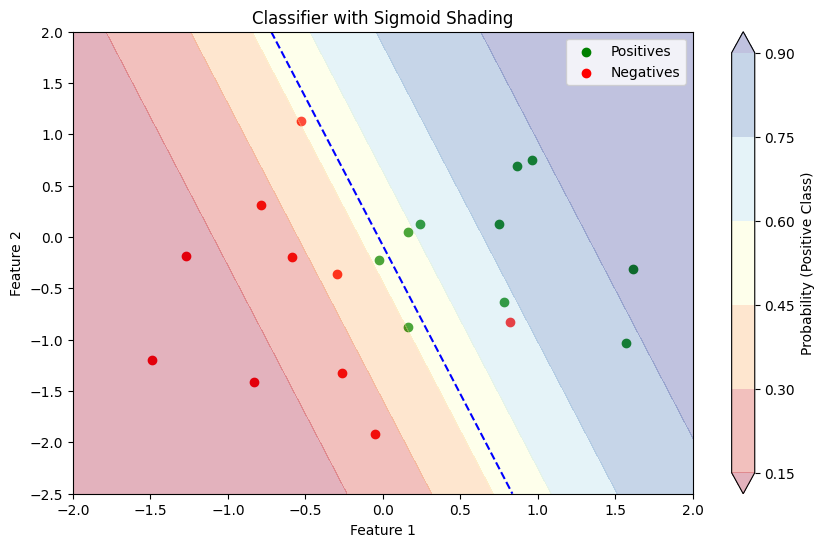
Figure 4: Classifier with Sigmoid Shading
Figure 4: Classifier with Sigmoid Shading

Decision Boundary

  • Once, we have a classifier outputting a score \(0 < \hat{y} < 1\), we need to create a decision rule.
  • Let \(0 < t < 1\) be a threshold:
    • If \(\hat{y} > t\), \(\hat{y}\) is classified as positive
    • If \(\hat{y} < t\), \(\hat{y}\) is classified as negative
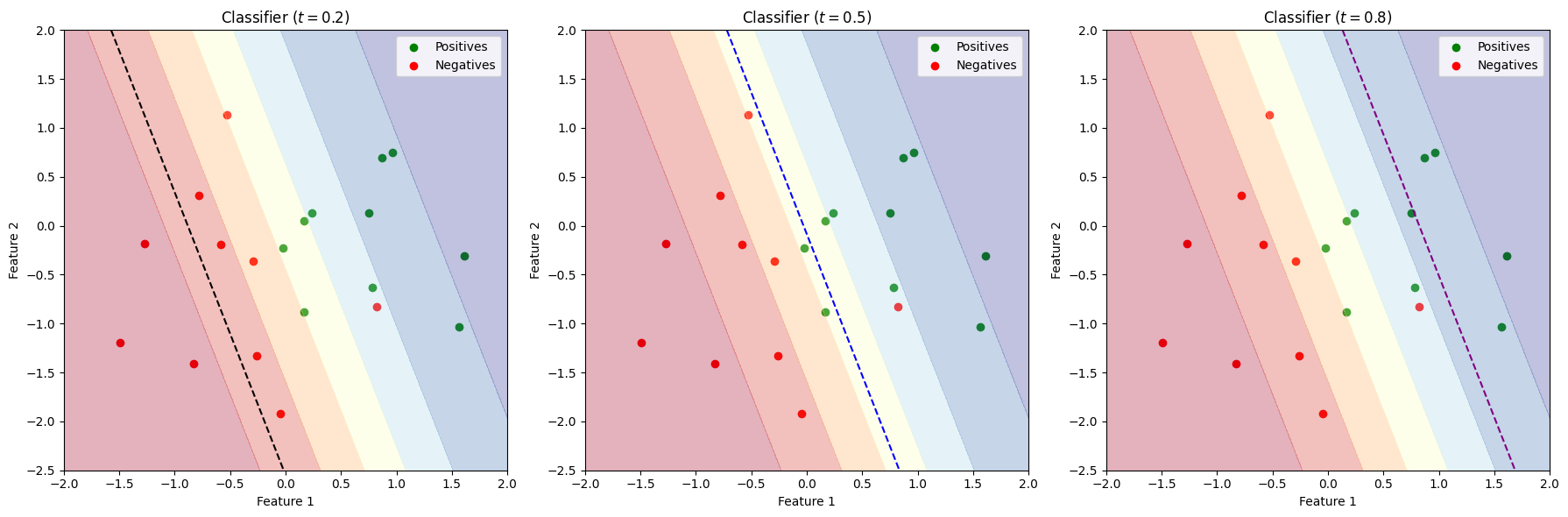
Figure 5: Changing Threshold
Figure 5: Changing Threshold

Performance metrics for a classifier:

  • Accuracy of a classifier: percentage of correct classification
  • Why accuracy alone is not a good measure for assessing the model?
    • Example: A rare disease occurs 1 in ten thousand people
    • A test that classifies everyone as free of the disease can achieve 99.999% accuracy when tested with people drawn randomly from the entire population

Types of Errors in Classification

  • Correct predictions:
    • True Positive (TP) : Predict \(\hat{y} = 1\) when \(y = 1\)
    • True Negative (TN) : Predict \(\hat{y} = 0\) when \(y = 0\)
  • Two types of errors:
    • False Positive/ False Alarm (FP): \(\hat{y} = 1\) when \(y = 0\)
    • False Negative/ Missed Detection (FN): \(\hat{y} = 0\) when \(y = 1\)

Metrics:

  • Sensitivity/Recall/TPR (How many positives are detected among all positive?)

    \[ \frac{\text{TP}}{\text{TP} + \text{FN}} \]

  • Precision (How many detected positives are actually positive?)

    \[ \frac{\text{TP}}{\text{TP} + \text{FP}} \]

Multiclass Classification

  • Previous Model:

    \[ f(x) = \sigma(\phi(x)w) \]

  • Representing Multiple Classses:
    • One-hot / 1-of-K vectors, ex : 4 Class
    • Class 1 : \(y = [1,0,0,0]\)
    • Class 2 : \(y = [0,1,0,0]\)
    • Class 3 : \(y = [0,0,1,0]\)
    • Class 4 : \(y = [0,0,0,1]\)

  • Multiple outputs:

    \[ f(x) = \text{softmax}(\phi(x)W) \]

  • Shape of \(\phi(x)W\): \((N, K) = (N, D) \times (D, K) \)

  • Softmax:

    \[ \text{softmax}(z_k) = \frac{e^{z_k}}{\sum_j e^{z_j}} \]

  • Softmax Example:

    \[ z = \begin{bmatrix}-1 \\ 2 \\ 1 \\ -4 \end{bmatrix} \]

    \[ \text{softmax}(z) = \begin{bmatrix}\frac{e^{-1}}{e^{-1} + e^{2} + e^{1} + e^{-4}} \\ \frac{e^{2}}{e^{-1} + e^{2} + e^{1} + e^{-4}} \\ \frac{e^{1}}{e^{-1} + e^{2} + e^{1} + e^{-4}} \\ \frac{e^{-4}}{e^{-1} + e^{2} + e^{1} + e^{-4}} \end{bmatrix} \approx \begin{bmatrix}0.035 \\ 0.704 \\ 0.259 \\ 0.002 \end{bmatrix} \]

Cross-entropy

  • Multple Outputs: \( \hat{y_i} = \text{softmax}(\phi(x_i)W)\)

  • Cross-Entropy:

    \[ J(W) = - \sum^{N}_{i=1} \sum^{K}_{k=1} y_{ik} \log (\hat{y_{ik}}) \]

  • Example, \(K = 4\), if \(y_i = [0, 0, 1, 0]\) then,

    \[ \sum^{K}_{k=1} y_{ik} \log (\hat{y_{ik}}) = \log (\hat{y_{i3}}) \]

Demos

  1. Diagnosing Breast Cancer
  2. Iris Dataset

References