NYU K12 STEM Education: Machine Learning (Day 3)

nyu-header

Polynomial Fitting

  • We have been using straight lines to fit our data. But it doesn’t work well every time
  • Some data have more complex relation that cannot be fitted well using a straight line
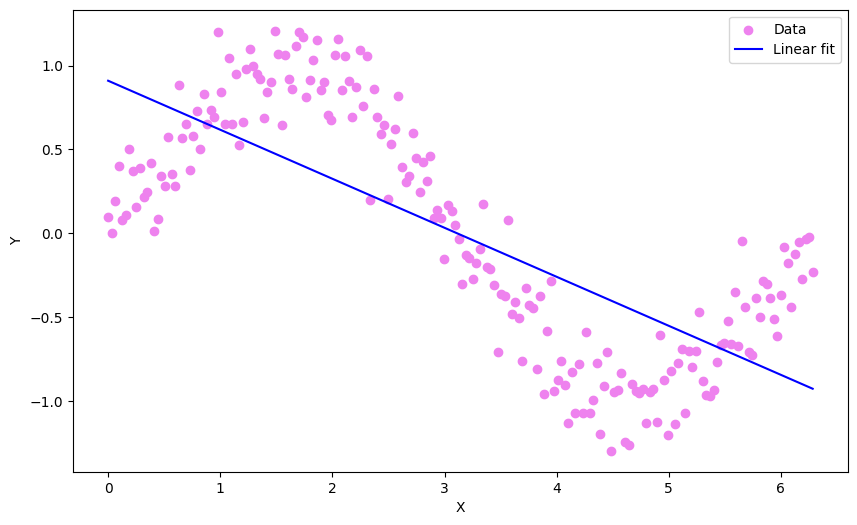
Figure 1: Complex Datasets
Figure 1: Complex Datasets

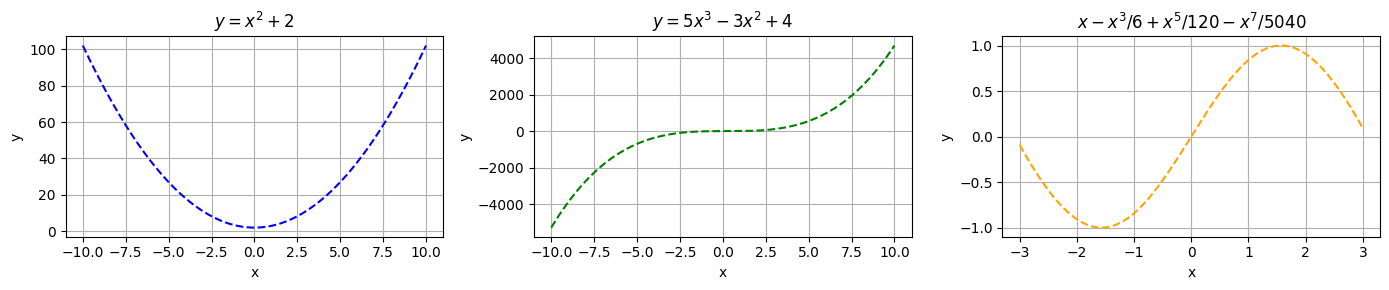
  • Polynomial: A sum of different powers of a variable

    Examples: \(y = x^2 + 2, y = 5x^3 − 3x^2 + 4\)

Figure 2: Polynomial Example
Figure 2: Polynomial Example
  • Polynomials of \(x\): \(\hat{y} = w_0 + w_1x +w_2x^2 + w_3x^3 + \cdots + w_Mx^M\)
  • \(M\) is called the order of the polynomial.
  • The process of fitting a polynomial is similar to linearly fitting multivariate data.
  • Rewrite in matrix-vector form \[ \begin{bmatrix} \hat{y_1} \\ \hat{y_2} \\ \vdots \\ \hat{y_N} \end{bmatrix} = \begin{bmatrix}1 & x_{1} & x_{1}^2 & \cdots & x_{1}^M \\ 1 & x_{2} & x_{2}^2 & \cdots & x_{2}^M \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{N} & x_{N}^2 & \cdots & x_{N}^M\end{bmatrix} \begin{bmatrix}w_0 \\ w_1 \\ \vdots \\ w_M \end{bmatrix} \]
  • This can still be written as: \(\hat{Y} = Xw\)
  • Loss: \[ J(w) = \frac{1}{N} ||Y - Xw ||^2 \]
  • The \(i^{th}\) row of the design matrix \(X\) is simply a transformed feature: \[ \phi(x_i) = (1, x_i, x_i^2, \cdots, x_i^M) \]
  • Original Design Matrix: \[ \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_N \end{bmatrix} \]
  • Design matrix after feature transformation: \[ \begin{bmatrix}1 & x_{1} & x_{1}^2 & \cdots & x_{1}^M \\ 1 & x_{2} & x_{2}^2 & \cdots & x_{2}^M \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{N} & x_{N}^2 & \cdots & x_{N}^M\end{bmatrix} \]
  • For the polynomial fitting, we just added columns of features that are powers of the original feature.

Overfitting

  • We learned how to fit our data using polynomials of different order
  • With a higher model order, we can fit the data with increasing accuracy
  • As you increase the model order, at certain point it is possible find a model that fits your data perfectly (ie. zero error)
  • What could be the problem?
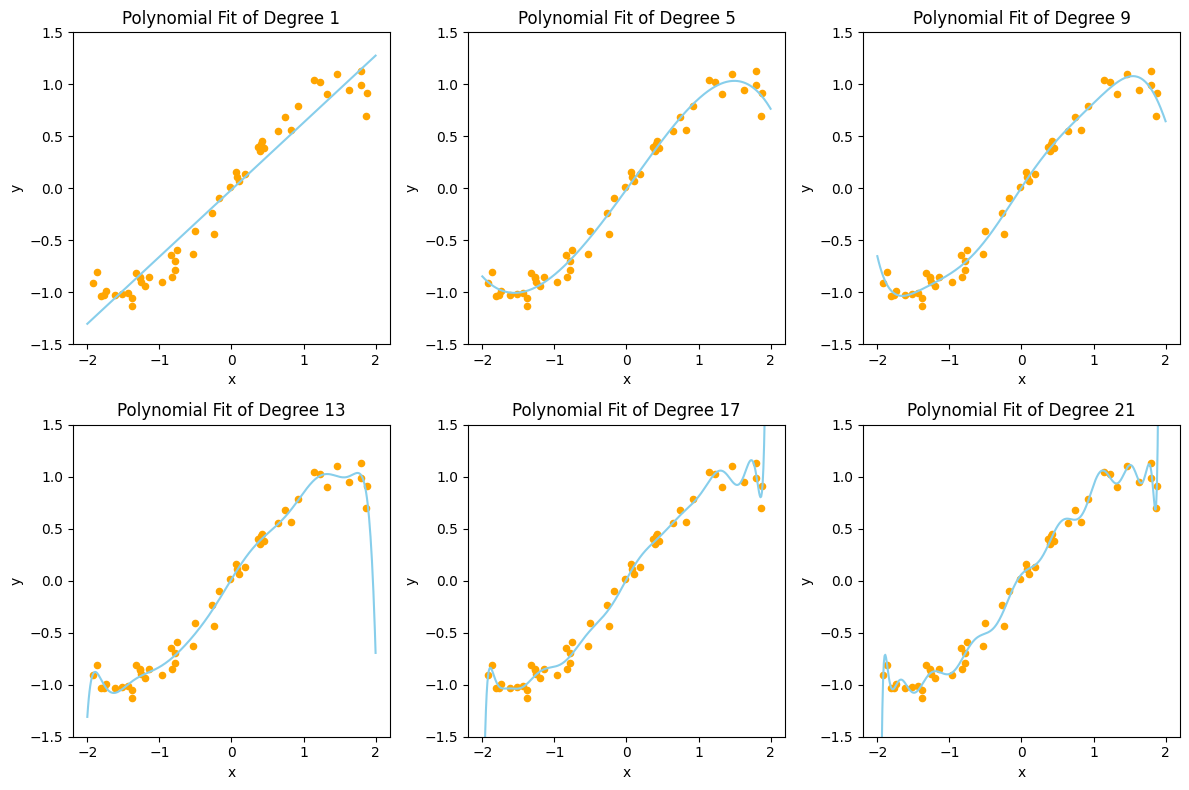
Figure 3: Overfitting Visualization
Figure 3: Overfitting Visualization
  • Which of these model do you think is the best? Why?
  • The problem is that we are only fitting our model using data that is given
  • Data usually contains noise
  • When a model becomes too complex, it will start to fit the noise in the data
  • What happens if we apply our model to predict some data that the model has never seen before? It will not work well.
  • This is called over-fitting.
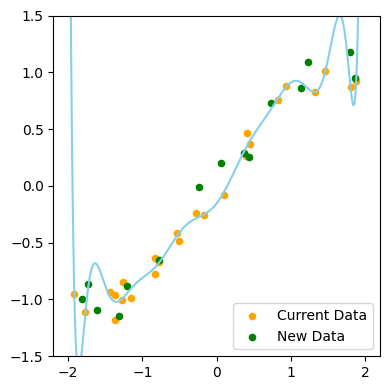
Figure 4: Overfitting on Current Data
Figure 4: Overfitting on Current Data
  • Split the data set into a train set and a test set
  • Train set will be used to train the model
  • The test set will not be seen by the model during the training process
  • Use test set to evaluate the model when a model is trained
  • With the training and test sets shown, which one do you think is the better model now?
Figure 5: Train and Test Data Split
Figure 5: Train and Test Data Split

Train and Test Error

  • Plot of train error and test error for different model order
  • Initially both train and test error go down as model order increase
  • But at a certain point, test error start to increase because of overfitting
Figure 6: Train and Test Losses
Figure 6: Train and Test Losses

Regularization

  • Regularization: methods to prevent overfitting
  • Is there another way?
    • Solution: We can change our cost function.

Weight Based Regularization

  • Looking back at the polynomial overfitting
  • Notice that weight-size increases with overfitting
Figure 7: Weight Sizes increase with Overfitting Figure 7: Weight Sizes increase with Overfitting
Figure 7: Weight Sizes increase with Overfitting

New Cost Function: \[ J(w) = \frac{1}{N} ||Y - Xw ||^2 + \lambda ||w||^2 \]

  • Penalize complexity by simultaneously minimizing weight values.
  • We call \(\lambda\) a hyper-parameter
  • \(\lambda\) determines relative importance
Figure 8: Weight Based Regularization
Figure 8: Weight Based Regularization

Tuning Hyper-parameters

  • Motivation: never determine a hyper-parameter based on training data
  • Hyper-Parameter: a parameter of the algorithm that is not a model-parameter solved for in optimization. Example: \(\lambda\) weight regularization value vs. model weights (\(w\))
  • Solution: split dataset into three
    1. Training set: to compute the model-parameters (\(w\))
    2. Validation set: to tune hyper-parameters (\(\lambda\))
    3. Test set: to compute the performance of the algorithm (MSE)

Non-linear Optimization

  • Cannot rely on closed form solutions
    • Computation efficiency: operations like inverting a matrix is not efficient
    • For more complex problems such as neural networks, a closed-form solution is not always available
  • Need an optimization technique to find an optimal solution
    • Machine learning practitioners use gradient-based methods

Gradient Descent Algorithm

  • Update Rule:

    \[ \text{Repeat\{} \\ w_{\text{new}} = w - \alpha \nabla J(w) \\ \text{\}} \]

Figure 9: Gradient Descent Illustration
Figure 9: Gradient Descent Illustration

General Loss Function Contours

  • Most loss function contours are not perfectly parabolic
  • Our goal is to find a solution that is very close to global minimum by the right choice of hyper-parameters
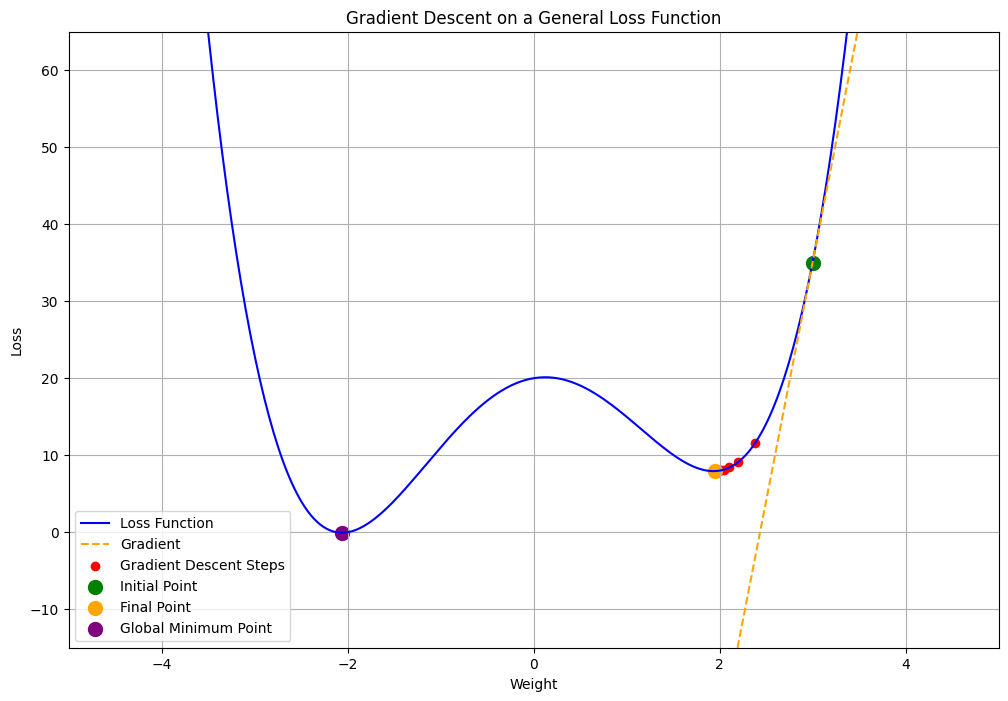
Figure 9: Gradient Descent on General Loss Curve
Figure 9: Gradient Descent on General Loss Curve

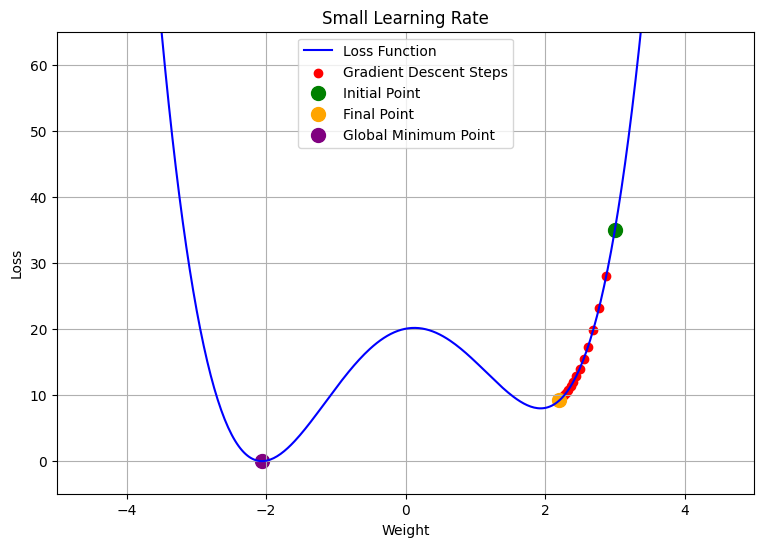
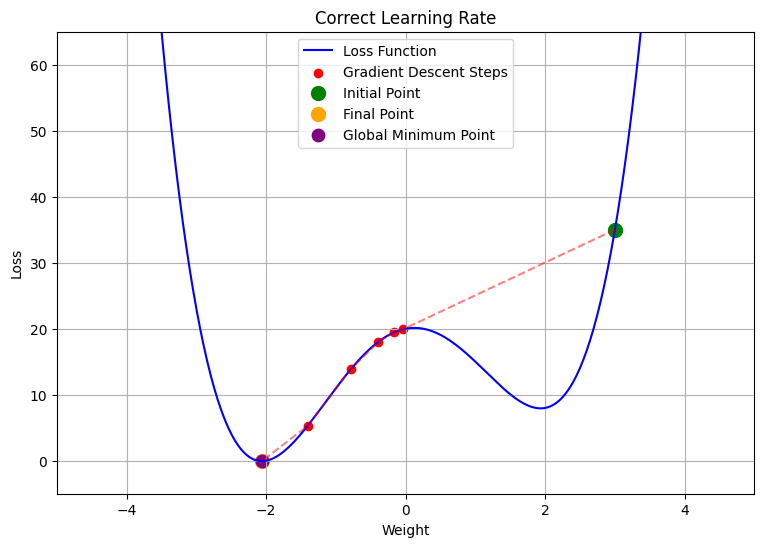
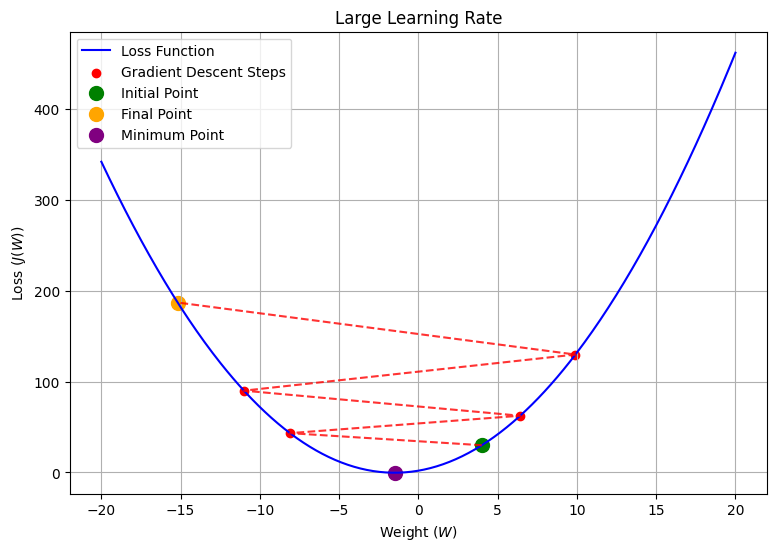
Understanding Learning Rate

  • Small Learning Rate:
Figure 10: Gradient Descent with Small Learning Rate
Figure 10: Gradient Descent with Small Learning Rate
  • Correct Learning Rate:
Figure 11: Gradient Descent with Correct Learning Rate
Figure 11: Gradient Descent with Correct Learning Rate
  • Large Learning Rate:
Figure 12: Gradient Descent with Large Learning Rate
Figure 12: Gradient Descent with Large Learning Rate

Some Learning Rate Animations:

  • Small Learning Rate:
  • Correct Learning Rate:
  • Large Learning Rate:

Demos

References