NYU K12 STEM Education: Machine Learning (Day 2)

nyu-header

Statistics Review

In machine learning, a solid understanding of basic statistical concepts is essential for analyzing data and interpreting model results.

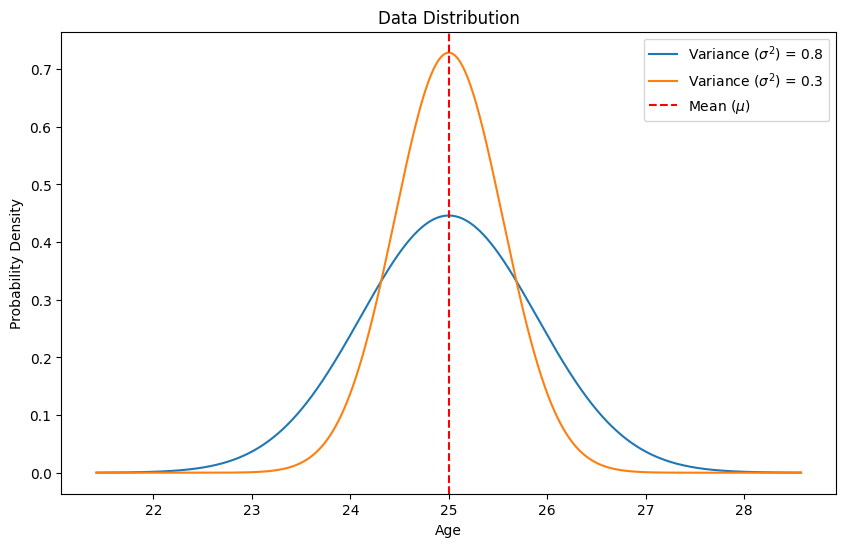
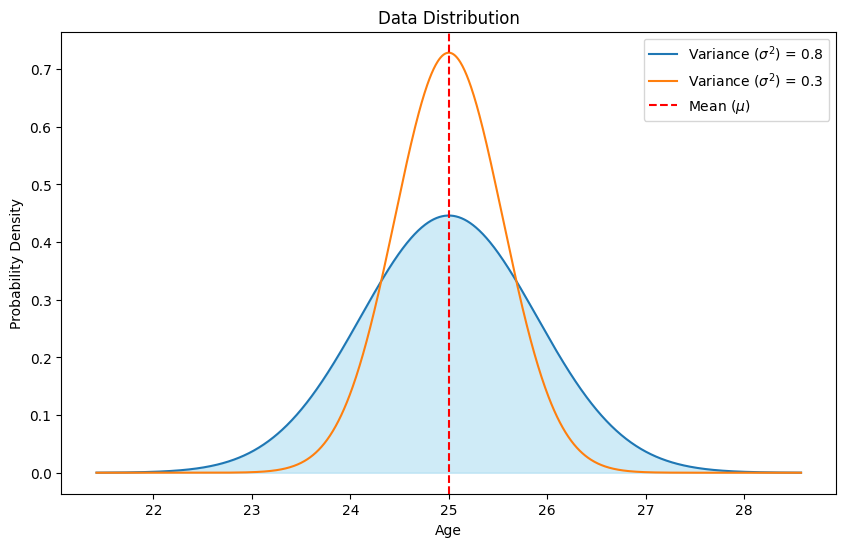
Mean

The mean, or average, is the sum of all the values in a dataset divided by the number of values. It provides a measure of the central tendency of the data.

Formula: \[ \text{Mean} (\mu) = \frac{1}{N} \sum_{i=1}^{N} x_i \]

Example:

For the dataset [2, 4, 6, 8, 10]: \[ \mu = \frac{2 + 4 + 6 + 8 + 10}{5} = 6 \]

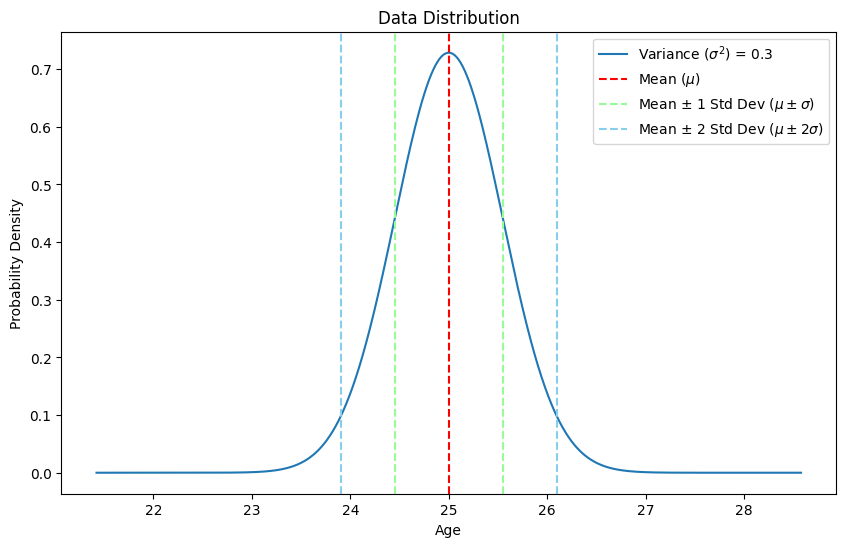
Variance

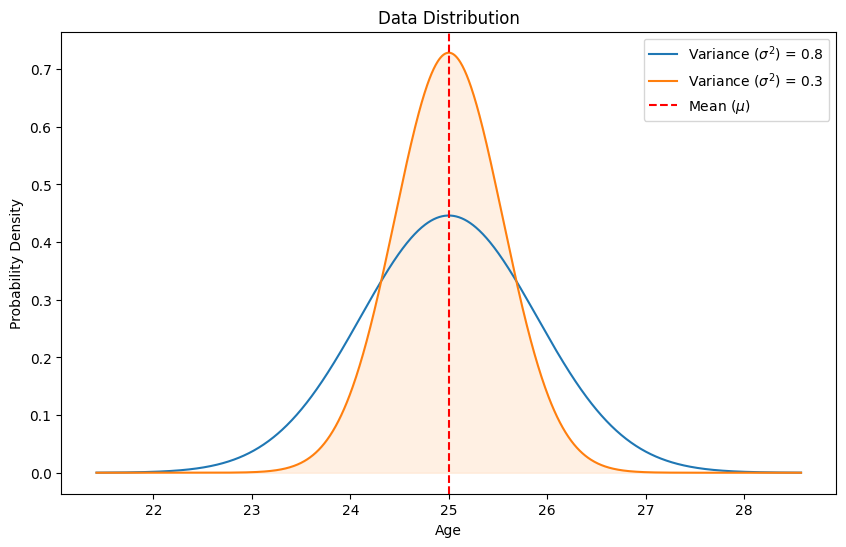
Variance measures the spread of the data points around the mean. It indicates how much the data varies from the mean.

Formula: \[ \text{Variance} (\sigma^2) = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2 \]

Example:

For the dataset [2, 4, 6, 8, 10]: \[ \sigma^2 = \frac{(2-6)^2 + (4-6)^2 + (6-6)^2 + (8-6)^2 + (10-6)^2}{5} = 8 \]

Mean and Variance Visualization

Figure 1: Mean and Variance Visualized
Figure 1: Mean and Variance Visualized
Figure 2: Wide Spread Dataset
Figure 2: Wide Spread Data
Figure 3: Less Spread Data
Figure 3: Less Spread Data

Standard Deviation

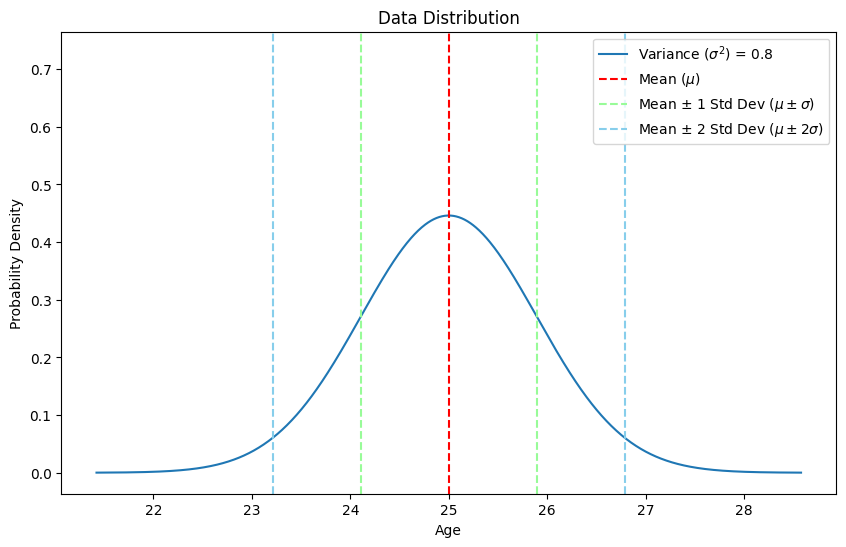
Standard deviation is the square root of the variance. It provides a measure of the spread of the data points in the same units as the data itself.

Formula: \[ \text{Standard Deviation} (\sigma) = \sqrt{\text{Variance}} \]

Example:

Using the variance calculated above: \[ \sigma = \sqrt{8} \approx 2.83 \]

Standard Deviation Visualization

Figure 4: Standard Deviation visualized on wide spread dataset
Figure 4: Standard Deviation visualized on wide spread dataset
Figure 5: Standard Deviation visualized on less spread dataset
Figure 5: Standard Deviation visualized on less spread dataset

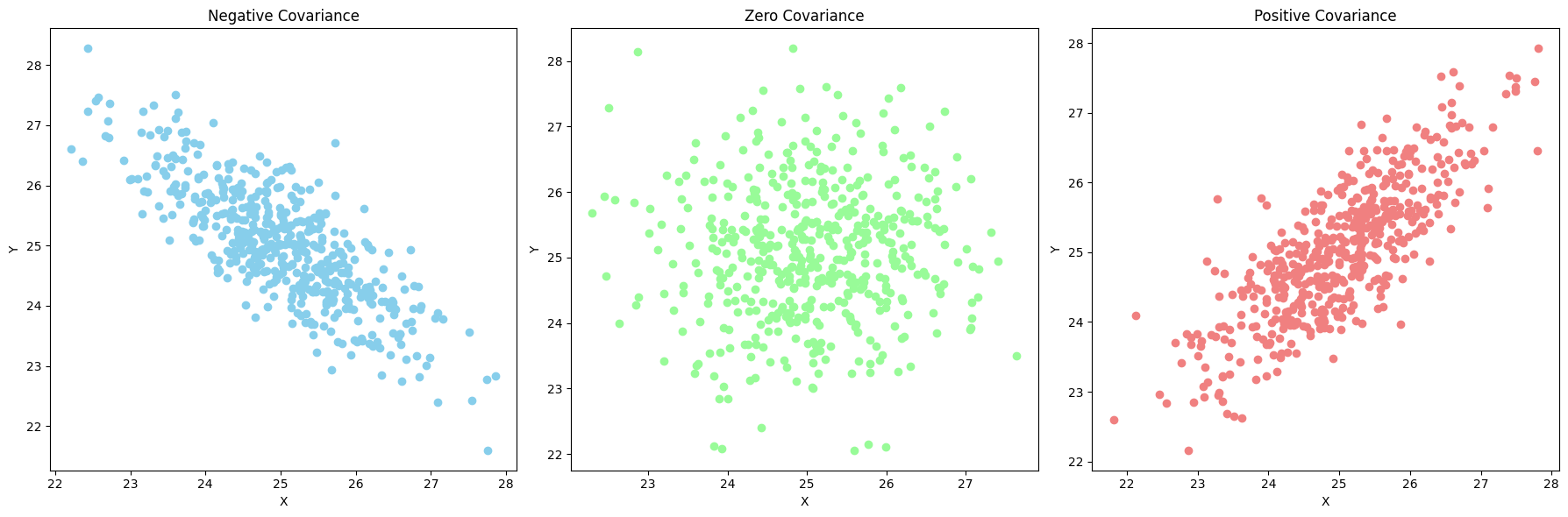
Covariance

Covariance measures the degree to which two variables change together. If the covariance is positive, the variables tend to increase together; if negative, one variable tends to increase when the other decreases.

Formula: \[ \text{Covariance} (\text{Cov}(X, Y)) = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu_X)(y_i - \mu_Y) \]

Example: For the datasets X = [2, 4, 6] and Y = [3, 6, 9]: \[ \text{Cov}(X, Y) = \frac{(2-4)(3-6) + (4-4)(6-6) + (6-4)(9-6)}{3} = 6 \]

Figure 6: Covariance visualized
Figure 6: Covariance visualized

Linear Regression

In a Nutshell…

  • Consider a function \(y = 2x + 1 \)
  • Here we introduce a new notation \(f (x) = 2x + 1 \)
  • What this means is that we have a function \(f (x ) \) which has \(x\) as its variable.
  • If we have different \(x\) values we will have different values of \(f(x)\). Example:
    • For \(f (x) = 2x + 1 \) and setting \(x = 1\) we have \(f (x) = 3\)
    • For \(f (x) = 2x + 1 \) and setting \(x = 0\) we have \(f (x) = 1\)
    • For \(f (x) = 2x + 1 \) and setting \(x = −1.5\) we have \(f (x) = −2\)
  • We believe that dataset are representation of underlying models which can be represented as functions of features.
  • For example, we can build a model to forecast weather, we can use the features humidity, current temperature and wind speed to estimate what the temperature will be tomorrow.
  • Here we have \(f (x)\) representing the tomorrow’s temperature and \(x\) being a vector containing humidity, current temperature and wind speed.
  • But many times we do have \(f (x)\) available, our task here is to figure out what \(f (x)\) is using the data available to us.
  • Here \(f (x)\) is called a model.
  • In other words, we want to find a model that fits the data.
  • It would be easier to have a ”framework” of the model ready and find the model parameters using the data.
    • \(f (x) = w_1x + w_0\)
    • \(f (x) = w_2x^2 + w_1x + w_0\)
    • \(f (x) = \frac{1}{e^{−(w_1x+w_0)} + 1}\)
  • The numbers \(w_0\), \(w_1\) and \(w_2\) are called model parameters.
  • We often write the model as \(f (x ; w)\), stacking all parameters to a vector \(w\).

Structure of a dataset

  • In a dataset we have many data.
  • We can represent each piece of data as \((x_i,y_i)\), \(i = 1,2,3,\cdots\)
  • \(x_i\) is called the feature and \(y_i\) is called the label.
  • The relationship between \(x_i\) and \(y_i\) and the model \(f\) is \(f (x_i ) = y_i\)
  • For example, if the weather forecast says it will be 21\(^{\circ}\)C (69.8\(^{\circ}\)F) if it turns out to be 22\(^{\circ}\)C (71.6\(^{\circ}\)F) you won’t be yelling at the TV.

How would you fit a line?

Can you find a line that passes through (0, 0) and (1, 1)?

  • The ”framework” of the model is \(f (x) = w_1x + w_0\)
  • The data is (\(x = 0\), \(f (x ) = y = 0\)) and (\(x = 1\), \(f (x ) = y = 1\)).
  • The process of finding a model to fit the data is to find the values of \(w_1\) and \(w_0\).

How would you fit a quadratic curve?

Can you find a quadratic curve that passes through (0, 0), (1, 1) and (−1, 1)?

  • The ”framework” of the model is \(f (x) = w_2x^2 + w_1x + w_0\)
  • The data is \((x = 0, f (x ) = y = 0)\), \((x = 1, f (x ) = y = 1)\) and \((x =−1,f(x)=y =1)\)
  • The process of finding a model to fit the data is to find the values of \(w_2\), \(w_1\) and \(w_0\).

Is Your Model a Good Fit?

  • How would you determine if your model is a good fit or not?
    • How will you determine this?
    • Is there a quantitative way?
  • We now introduce a new notation \(f(x_i) = \hat{y_i}\) here the \(\hat{\cdot}\) represents \(f(x_i)\) is a prediction of \(y_i\).

Error Functions

  • An error function quantifies the discrepancy between your model and the data.
    • They are non-negative, and go to zero as the model gets better.
  • Common Error Functions:
    • Mean Squared Error: \[ \text{MSE} = \frac{1}{N}\sum^{N}_{i=1}||y_i - \hat{y_i}||^2 \]
    • Mean Absolute Error: \[ \text{MAE} = \frac{1}{N}\sum^{N}_{i=1}|y_i - \hat{y_i}| \]
  • In later units, we will refer to these as cost functions or loss functions.

Linear Regression

  • Linear models: For scalar-valued feature \(x\), this is \(f (x) = w_1x + w_0\)
  • One of the simplest machine learning model, yet very powerful.

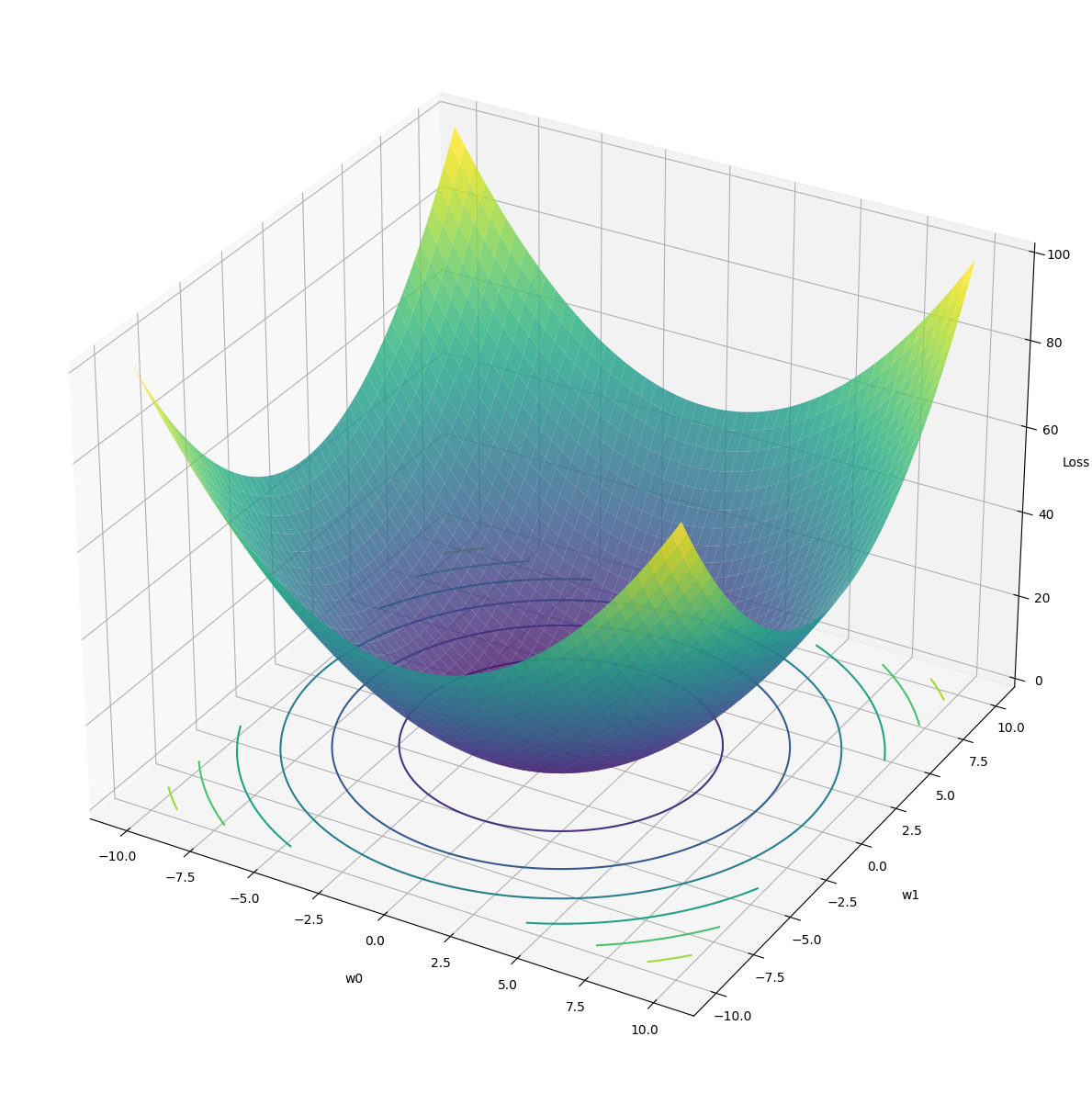
Least Square Solution

  • Model: \(f (x) = w_1x + w_0\)
  • Loss: \[ J(w_0, w_1) = \frac{1}{N}\sum^{N}_{i=1}||y_i - f(x_i)||^2 \]
  • Optimization: Find \(w_0\), \(w_1\) such that \(J(w_0, w_1)\) is the least possible value (hence the name “least square”).
Figure 7: Loss Landscape
Figure 7: Loss Landscape

Using Pseudo-Inverse

  • For \(N\) data points (\(x_i, y_i\)) we have, \[ \begin{split} \hat{y_1} &= w_0 + w_1x_1 \\ \hat{y_2} &= w_0 + w_1x_2 \\ &\vdots \\ \hat{y_N} &= w_0 + w_1x_N \end{split} \]
  • In matrix form we have, \[ \begin{bmatrix}\hat{y_1} \\ \hat{y_2} \\ \vdots \\ \hat{y_N} \end{bmatrix} = \begin{bmatrix} 1 & x_1 \\ 1 & x_2 \\ \vdots & \vdots \\ 1 & x_N \end{bmatrix} \begin{bmatrix}w_0 \\ w_1 \end{bmatrix} \]
  • We can write it as \(\hat{Y} = X \times w \). We call \(X\) the design matrix.
  • We can put the desired labels in matrix form as well: \[ Y = \begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_N \end{bmatrix} \]
  • Our goal is to minimize the error between \(Y\) and \(\hat{Y}\) which can be written as \(||Y - \hat{Y}||^2\)

Multilinear Regression

  • What if we have multivariate data with \(x\) being a vector?

  • Example: \[ x_i = \begin{bmatrix}x_{i1} \\ x_{i2} \end{bmatrix} \]

    \[ \begin{split} \hat{y_1} &= w_0 + w_1x_{11} + w_2x_{12} \\ \hat{y_2} &= w_0 + w_1x_{21} + w_2x_{22} \\ &\vdots \\ \hat{y_N} &= w_0 + w_1x_{N1} + w_2x_{N2} \end{split} \]

  • The model can be written as: \( \hat{y_i} = \begin{bmatrix}1 & x_{i1} & x_{i2}\end{bmatrix} \begin{bmatrix}w_0 \\ w_1 \\ w_2 \end{bmatrix} \)
  • In matrix-vector form: \( \begin{bmatrix} \hat{y_1} \\ \hat{y_2} \\ \vdots \\ \hat{y_N} \end{bmatrix} = \begin{bmatrix}1 & x_{11} & x_{12} \\ 1 & x_{21} & x_{22} \\ \vdots & \vdots & \vdots \\ 1 & x_{N1} & x_{N2}\end{bmatrix} \begin{bmatrix}w_0 \\ w_1 \\ w_2 \end{bmatrix} \)
  • Solution remains the same \(w = (X^T X)^{-1} X^T Y\)

Demos

  1. Vectorized Programming
  2. Plotting Functions
  3. Ice-breaker Dataset
  4. Linear Regression
  5. Multivariable Linear Regression

References